 拡大
拡大
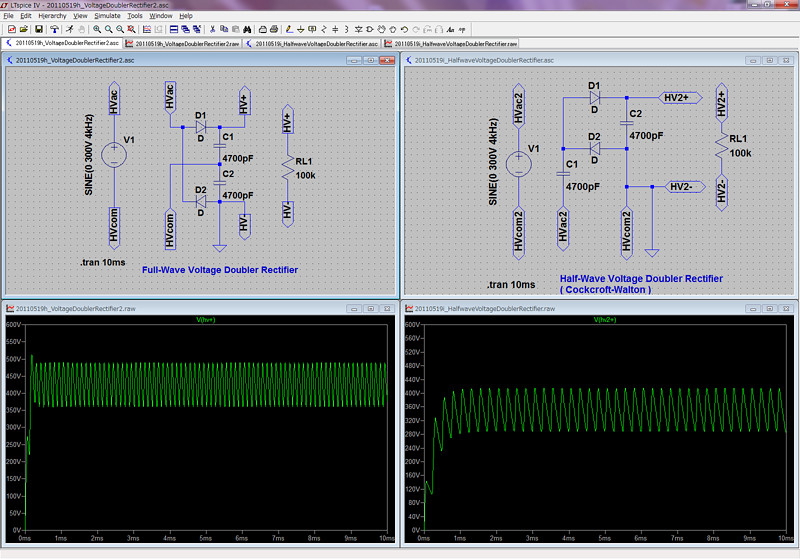
LTspice で倍電圧整流をシミュレートしてみました。
回路の詳しい解説は、たとえば、
ガイガー管を動かそうと、写ルンですの基板を取り出して高電圧発生部(300 V 前後か?)から電圧を上げて整流していたのですが、整流方法によって電源の強さがだいぶ異なるように感じました。 高校の物理で、コンデンサーからコンデンサーに充電すると電力を消費するのでエネルギー保存則で計算できないと習ったようなおぼろげな記憶があります。 倍電圧でない整流回路でも、全波整流と半波整流では取り出せる電流が違うので、名前からも推測できます。
SPICE モデルでのコンデンサや抵抗の定数はいいかげんに決めてあります。 高耐圧のコンデンサで容量が大きなものは入手しにくいので、手持ちの 472 = 4700 pF を仮定しました。 ガイガー管の回路を想定すると、負荷抵抗は GΩ 以上あると思いますが、わかりやすさのために消費電力を大きめに見積もって 100 kΩ としました。
交流電源が 300 V なので出力は倍の 600 V になって欲しいところですが、 負荷抵抗の消費電力が大きすぎるのでだいぶ電圧降下しています。 それでも、半波整流より全波整流のほうが電圧が高くなっています。
また、電源投入時の過渡特性も全波整流のほうがすぐに立ち上がっています。 半波整流のほうでは、負荷抵抗を外して開放にしても立ち上がりに時間がかかります。 半波整流のほうはコッククロフト・ウォルトン回路の動作を考えても、電荷を高電圧側のコンデンサに持ち上げていく動作になるので、当然といえば当然です。
もっとも、全波整流のほうは、倍電圧のプラスとマイナスが接地されないという問題があります。 しかし、ガイガーカウンターの実験用ならばかまわないと割り切ることはできます。
なお、英語で全波(半波)倍電圧整流のことを何というのか分かりません。 英語の感覚として、なんとなく変な表現になっているような気がしますが、 とりあえず自分で何の記事・回路か分かればいいということで、そのままにしてあります。Google で候補を探ると、倍電流整流という表現がヒットしてくるようです。